Les techniques laser appliquéees à
l'aérodynamique expérimentale.
Deux ouvrages en français :
- Vélocimétrie laser.     
- Techniques laser.     

1 - AILE, PORTANCE, TRAINEE, SILLAGE ?

À la question " pourquoi un avion vole ? ", on trouve plusieurs réponses qui soulignent un des aspects de la même réalité :

• L’air est dévié vers le bas par la présence de l’aile et la troisième loi de Newton (action => réaction en sens opposé) explique la présence d’une force orientée vers le haut exercée sur l’aile. C’est vrai et on va le démontrer plus loin.

• La vitesse de l’air U est plus grande à l’extrados ¹ qu’à l’intrados ². La loi de Bernoulli (1700-1782) qui dit que p + ½ .U² = Constante implique que la pression p à l’extrados est inférieure à la pression sur l’intrados et donc que l’aile est " aspirée " vers le haut. Pour expliquer cette différence de vitesse entre l’extrados et l’intrados on dit que les particules de gaz parcourant l’extrados ont une plus grande distance à couvrir pour atteindre le bord de fuite ³ que les particules parcourant l’intrados. Certains rétorquent que pour un profil d’aile symétrique la distance est la même et que cette affirmation est fausse. Si on parle de la distance du point d'arrêt de bord d'attaque au point d'arrêt du bord de fuite, la distance est en général plus longue à l'extrados. Ceci n'a pas grande importance puisque les temps de parcours des particules fluides sont différents (excepté dans le cas du cylindre). Les particules passant par l'intrados arrivent au bord de fuite en retard par rapport à celles qui passent par l'extrados.

• L’air tourne autour de l’aile et cela crée un tourbillon parallèle à l’envergure (tourbillon " attaché " à l’aile analogue à un courant électrique) qui sous l’action de la vitesse relative (analogue à un champ magnétique) produit une force vers le haut analogue à la loi d’Ampère. C’est la base de la théorie de la " ligne portante " de Prandtl.

En fait ce n'est pas localement qu'il faut chercher la cause de la portance car (pour un écoulement incompressible) c'est la totalité du fluide qui s'organise pour contourner l'obstacle constitué par l'aile.
Une petite perturbation très localisée introduite dans un fluide supposé incompressible "dérange" instantannément la totalité du fluide jusqu'à l'infini.

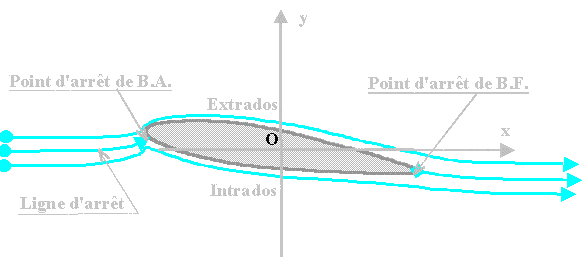
Figure 1 : Schéma de l’écoulement "2D" autour d’un profil.

Ces questions ne sont pas spécifiques aux avions, mais elles se posent de la même manière si on s’intéresse à la force qui fait avancer un voilier. Bien que leur épaisseur soit très petite (quoique certains voiliers de course aient maintenant des voiles " épaisses "), les voiles se comportent comme des ailes. De plus, pourquoi un voilier n’est-il pas poussé sur l’eau comme un bouchon mais est capable de naviguer contre le vent ? C’est que la (ou les) dérive du bateau subit sous l’eau une force semblable à la poussée exercée par l’air sur les voiles ou sur une aile plongée dans l’eau.

¹ L’extrados est la surface " sous le vent " et ² l’intrados est la surface de l’aile qui fait face majoritairement au vent relatif, les marins disent surface " au vent ". Cette définition est claire si on imagine un profil d’aile ou une voile placée à une grande incidence.

³ Si on suit les trajectoires de particules d’air arrivant sur l’aile, une partie passe du coté extrados, l’autre coté intrados. La ligne qui sépare ces deux cotés est " la ligne d’arrêt ". En effet les particules fluides qui suivent cette ligne ne glissent pas autour du profil mais " hésitent " en arrivant sur le profil d’aile et s’arrêtent vers le bord d’attaque. Ce point particulier du bord d’attaque est le " point d’arrêt de bord d’attaque " ou point d’arrêt amont. Pour la plupart des profils, on démontre qu’il existe un " point d’arrêt de bord de fuite " à l’extrémité aval de l’aile, pourvu que l’angle aigu que font les surface extrados et intrados ne soit pas nul, ce qui est le cas dans la réalité.

La lettre grecque " " (rho) est la masse volumique de l’air (qui dépend de la pression p et de la température T) voisine de 1.3 kg/m³ dans les conditions " normales " T=293 K, p=1013 hP (P = Pascal), U est la vitesse de l’air (m/s).

Les quatre grandeurs physiques (p, T, , U) dépendent bien entendu de l’endroit où on est dans l’écoulement. S’il n’y a pas d’apport de chaleur les variations de et de T sont proportionnelles à M² où M=U/a est le nombre de Mach local de l’écoulement. " U " est la vitesse locale et " a " la célérité du son locale qui ne dépend que de la température (environ 330 m/s dans l’air et 1500 m/s dans l’eau).

Pour les petits avions et les voiliers, on peut négliger ces variations de et on considère que le fluide est incompressible : = Constante. On conservera cette hypothèse simplificatrice (qui n’est pas très restrictive) dans toute la suite. De plus on admettra que le temps ne fait rien à l’affaire (sauf pour la théorie générale) et que les écoulements sont donc stationnaires.

En réalité les particules fluides ne glissent pas sur l’aile. Celles qui sont " au contact " adhèrent à la paroi et ont une vitesse nulle par rapport à la surface de l’aile à cause de la viscosité. Cette zone près de la paroi où les particules sont ralenties du fait de la viscosité est nommée "couche limite". Pour un écoulement " propre " autour d’une aile d’avion la couche limite a une épaisseur très faible .

Figure 2 : Ecoulement autour d’un profil d’aile avec couche limite.

Si l’écoulement est laminaire cette épaisseur est proportionnelle à (1/Re)^1/2. . Elle dépend donc du nombre de Reynolds Re = U.L/ où L est une longueur caractéristique (la corde de l’aile) et (nu) la viscosité cinématique (1.5 10^-4 pour l’air dans les conditions normales). On négligera les effets de la viscosité dans la suite, ce qui revient à admettre que la couche limite existe mais qu’elle est d’épaisseur infiniment mince par rapport à la corde, l’épaisseur ou l’envergure de l’aile, de la voile...

On dit alors qu’on a un " fluide  parfait ". L'absence de viscosité simplifie considérablement le problème d'une aile qui se déplace dans un fluide parfait.
En effet, si l'aile se déplace dans de l'air au repos, il n'y a pas de rotation du fluide puisque c'est le frottement (dû à la viscosité près de la surface de l'aile) qui crée la rotation du fluide dans la couche limite comme c'est le frottement du pneu sur la route qui fait tourner la roue : sur du verglas (pas de frottement) la roue glisse sans tourner.
Cette hypothèse simplificatrice n’est plus acceptable pour des écoulements " décollés " comme par exemple pour une aile " décrochée " ou une voile " faseyante ".
On retiendra cette hypothèse simplificatrice ce qui nous permettra dans les 4 chapitres suivants (ce sont des fichiers .pdf téléchargeables) d'utiliser un domaine particulier de l'aérodynamique théorique à savoir la théorie des écoulements à potentiel de vitesse.

On traite d’abord au chapitre 2 le cas de l’écoulement bidimensionnel (2D) autour d’un cylindre placé transversalement dans un flux d’air. Pour suivre ces démonstrations il suffit d’avoir quelques connaissances en trigonométrie (sinus, cosinus) et sur les vecteurs (coordonnées cartésienne, polaire). Ce cas "académique" présente tous les aspects de l’écoulement autour d’un profil quelconque tout en permettant un calcul relativement simple.

De plus, on montre au chapitre 3 qu’à l’aide d’une transformation mathématique on peut calculer le cas de profils quelconques à partir de l’écoulement autour du cylindre. Les calculs sont un peu plus compliqués car on fait appel aux nombres complexes et à la transformation conforme (dont la transformation de Joukovski).

On y démontre que la portance, la déviation du flux en sens opposé (ou encore la rotation du flux), "l' aspiration" de l'aile à l'extrados due à la dépression causée par une vitesse de l'air à l'extrados supérieure à sa vitesse à l'intrados sont des phénomènes concomitents.

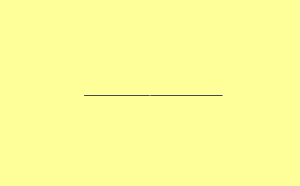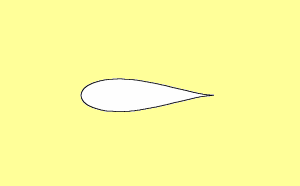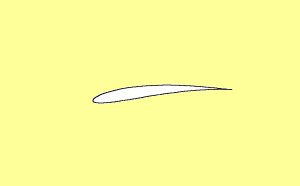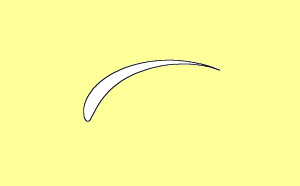
Figure 3 : Illustration montrant différents profils déduits du cercle par transformation de Joukovski.

Figure 4 : Trajectoires de particules fluides après un temps de parcours fixé.
Les particules "extrados" sont plus en aval que les particules "intrados".

L'origine du concept de "potentiel complexe" est précisée au chapitre 3+. On part des équations de base et on montre comment on en arrive à la notion de potentiel complexe et de transformation conforme.

On présente au chapitre 4 la théorie de la ligne portante de Prandtl pour les écoulements 3D.
Cette partie est plus difficile, mais on chemine pas à pas pour montrer comment cette théorie conduit à "l’aile elliptique" de la plupart des avions du milieu du 20 ème siècle.

Figure 5 : Animation montrant que l'aile du Supermarine Spitfire Mk 1 est elliptique.

On y montre aussi qu'on améliore la finesse d'une aile en augmentant son allongement (envergure/corde) et que l'intensité de la "turbulence de sillage" d'un avion est proportionnelle à son poids divisé par son envergure.

Figure 6 : Vus de l'arrière, les tourbillons de sillage : "turbulence".

Photo extraite du site www.airliners.net.

On aborde au chapitre 5 la théorie générale des écoulements incompressibles tridimensionnels à potentiel de vitesse. On précise les bases théoriques, on pose les équations du problème et on évoque la résolution par voie numérique. On termine sur deux exemples : une aile avec volets de courbure déployés et un rotor d’hélicoptère quadripale en vol stationnaire.

Enfin on termine avec la théorie des écoulements compressibles à potentiel de vitesse au chapitre 6. La différence essentielle est qu'alors une perturbation très locale introduite dans un écoulement compressible se propage à la vitesse du son dans l'écoulement et non pas instantanément (à une vitesse infinie) si on admet l'hypothèse d'incompressibilité du fluide, d'où certaines complications !
On présente le cas particulier de l'acoustique, l'écoulement dans une tuyère supersonique et le choc de recompression. Pour résoudre le problème des écoulements à potentiel de vitesse compressible (qui englobe donc l'acoustique) on fait appel à des théories mathématiques relativement récentes (théorie de distributions) et les calculs sont effectués dans le détail.
On montre ainsi pourquoi les avions de ligne modernes (comme le MD83) qui volent à un nombre de Mach transsonique M=0.8 ont des ailes en flèche et à relativement faible corde comparé aux avions de la deuxième guerre mondiale comme le Spitfire ou le F4U Corsair ou encore aux avions d'aéroclub.

Douglas MD83  et  Vought F4U Corsair